Running statistics on SNP markers
Overview
Teaching: 30 min
Exercises: 10 minQuestions
How can I analyze a SNP dataset in R?
Objectives
Calculate allele frequency, missing data rate, heterozygosity, and linkage disequilibrium.
Evaluate population structure using principal coordinates analysis
library(VariantAnnotation)
library(snpStats)
library(ggplot2)
library(scater)
library(magrittr)
Picking up where we left off in the last episode:
myvcf3 <- VcfFile("data/hmp321_agpv4_chr1_subset_filtered.vcf.bgz")
hdr <- scanVcfHeader(myvcf3)
all_sam <- samples(hdr)
keep_sam <- all_sam[!all_sam %in% c("32", "98F1")]
keep_regions <- GRanges(seqnames = "1",
ranges = IRanges(start = c(21.4e6, 22.9e6),
end = c(22.3e6, 23.8e6)))
names(keep_regions) <- c("Region_1", "Region_2")
svp <- ScanVcfParam(info = c("DP", "MAF"), geno = "GT",
samples = keep_sam, which = keep_regions,
fixed = "ALT")
mydata <- readVcf(myvcf3, param = svp, genome = seqlevels(keep_regions))
Converting from VCF to snpMatrix
The snpStats package has a number of functions for analyzing SNP data. It
uses its own class called SnpMatrix. Luckily there is a conversion function
for CollapsedVCF objects, which is what we have.
mysnpmat <- genotypeToSnpMatrix(mydata)
Warning in .local(x, ...): variants with >1 ALT allele are set to NA
non-single nucleotide variations are set to NA
mysnpmat
$genotypes
A SnpMatrix with 198 rows and 24528 columns
Row names: 2005-4 ... german_EZ5
Col names: 1-21094080 ... 1-23395848
$map
DataFrame with 24528 rows and 4 columns
snp.names allele.1 allele.2 ignore
<character> <DNAStringSet> <DNAStringSetList> <logical>
1 1-21094080 A G FALSE
2 1-21094095 C G FALSE
3 1-21094140 A G FALSE
4 1-21094172 G T FALSE
5 1-21094216 C T FALSE
... ... ... ... ...
24524 1-23395014 C T FALSE
24525 1-23395152 C T FALSE
24526 1-23395224 A G FALSE
24527 1-23395794 G A FALSE
24528 1-23395848 C T FALSE
The ignore column indicates markers that were ignored for having multiple
alleles, being insertions or deletions, or being coded in a non-diploid
fashion. Let’s also see how the genotypes are stored.
matrix(as.numeric(mysnpmat$genotypes[1:10,1:10]),
nrow = 10, ncol = 10)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 1 1 1 1 3 3 3 0
[2,] 1 1 1 1 1 1 3 1 3 0
[3,] 1 1 1 1 1 1 1 1 1 0
[4,] 1 1 1 3 1 1 3 1 1 0
[5,] 1 1 1 1 1 1 1 1 1 0
[6,] 1 1 1 1 1 1 3 1 1 0
[7,] 1 1 1 1 1 1 1 1 1 0
[8,] 1 1 1 1 1 1 1 1 1 0
[9,] 1 1 1 3 1 1 3 1 1 0
[10,] 1 1 1 1 1 1 3 1 1 0
In this case, 1 and 3 indicate homozygotes, 2 indicates a heterozygote, and 0 indicates missing data.
Reading from other formats
If you want to import to the snpStats package from other formats such as PED or PLINK, see the following vignette:
vignette("data-input-vignette", package = "snpStats")You can also use
write.plinkto export to PLINK format.
Basic statistics and filtering on SNPs
There’s not a lot of point to keeping SNPs that were all set to 0, so let’s
eliminate them using the ignore column.
mat <- mysnpmat$genotypes[,!mysnpmat$map$ignore]
mat
A SnpMatrix with 198 rows and 21136 columns
Row names: 2005-4 ... german_EZ5
Col names: 1-21094080 ... 1-23395848
The summary function give us an overview of the dataset. Here, “rows” are
samples and “cols” are SNPs.
summary(mat)
$rows
Call.rate Certain.calls Heterozygosity
Min. :0.8407 Min. :1 Min. :0.0001559
1st Qu.:0.9623 1st Qu.:1 1st Qu.:0.0013602
Median :0.9751 Median :1 Median :0.0024126
Mean :0.9662 Mean :1 Mean :0.0061321
3rd Qu.:0.9802 3rd Qu.:1 3rd Qu.:0.0043879
Max. :1.0000 Max. :1 Max. :0.1447796
$cols
Calls Call.rate Certain.calls RAF
Min. : 42.0 Min. :0.2121 Min. :1 Min. :0.00000
1st Qu.:192.0 1st Qu.:0.9697 1st Qu.:1 1st Qu.:0.05303
Median :195.0 Median :0.9848 Median :1 Median :0.13590
Mean :191.3 Mean :0.9662 Mean :1 Mean :0.25637
3rd Qu.:197.0 3rd Qu.:0.9949 3rd Qu.:1 3rd Qu.:0.42934
Max. :198.0 Max. :1.0000 Max. :1 Max. :0.95408
MAF P.AA P.AB P.BB
Min. :0.00000 Min. :0.04592 Min. :0.000000 Min. :0.00000
1st Qu.:0.05303 1st Qu.:0.56680 1st Qu.:0.000000 1st Qu.:0.05051
Median :0.13077 Median :0.86224 Median :0.005076 Median :0.13265
Mean :0.17412 Mean :0.74066 Mean :0.005942 Mean :0.25340
3rd Qu.:0.29124 3rd Qu.:0.94444 3rd Qu.:0.010204 3rd Qu.:0.42487
Max. :0.50000 Max. :1.00000 Max. :0.628571 Max. :0.95408
z.HWE
Min. :-14.071
1st Qu.:-13.928
Median :-13.626
Mean :-13.268
3rd Qu.:-13.166
Max. : 4.514
NA's :59
The “call rate” is the proportion of data that were non-missing. So, the
samples ranged from 0-16% missing data, and the SNPs ranged from 0-79%
missing data. 100% of calls were certain because we imported from the GT
field, but if we had imported from the GL field there would have been some
uncertainty. Each sample has a proportion heterozygosity called, which could
be used to confirm hybrid vs. inbred individuals or identify sample
contamination. Allele frequencies, per SNP, are expressed both with respect to
the ALT allele (RAF) and the minor allele (MAF). We have frequencies of
all three possible genotypes for a diploid. Lastly we have the z-statistic for
departure from Hardy-Weinberg Equilibrium.
Let’s look at per-sample data.
sample_stats <- row.summary(mat)
ggplot(sample_stats, aes(x = Call.rate, y = Heterozygosity)) +
geom_point()
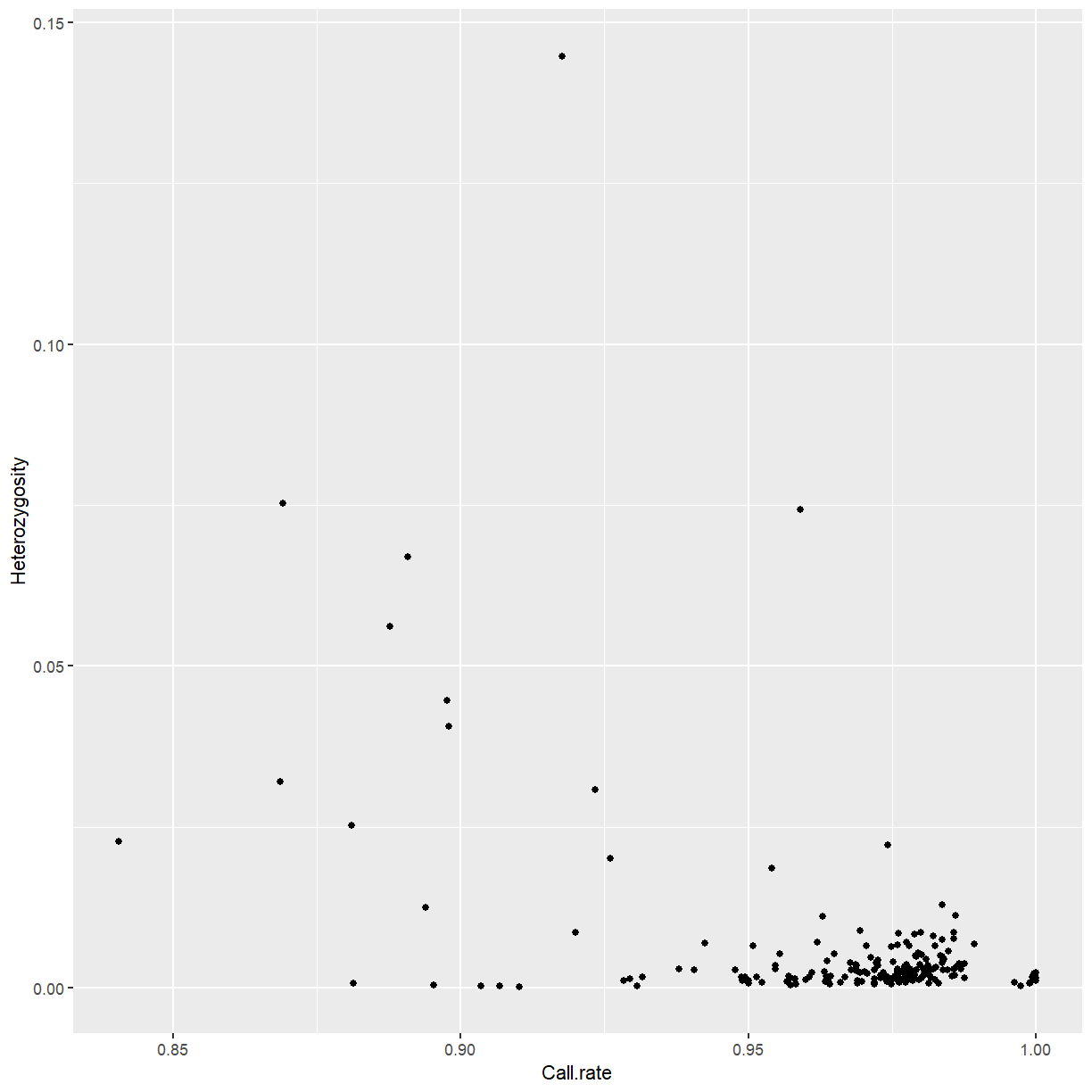
We’ll discard outliers for heterozygosity. In your own work, you might consider filtering by call rate as well.
highhet <- isOutlier(sample_stats$Heterozygosity, type = "higher")
ggplot(sample_stats, aes(x = Call.rate, y = Heterozygosity,
color = highhet)) +
geom_point()
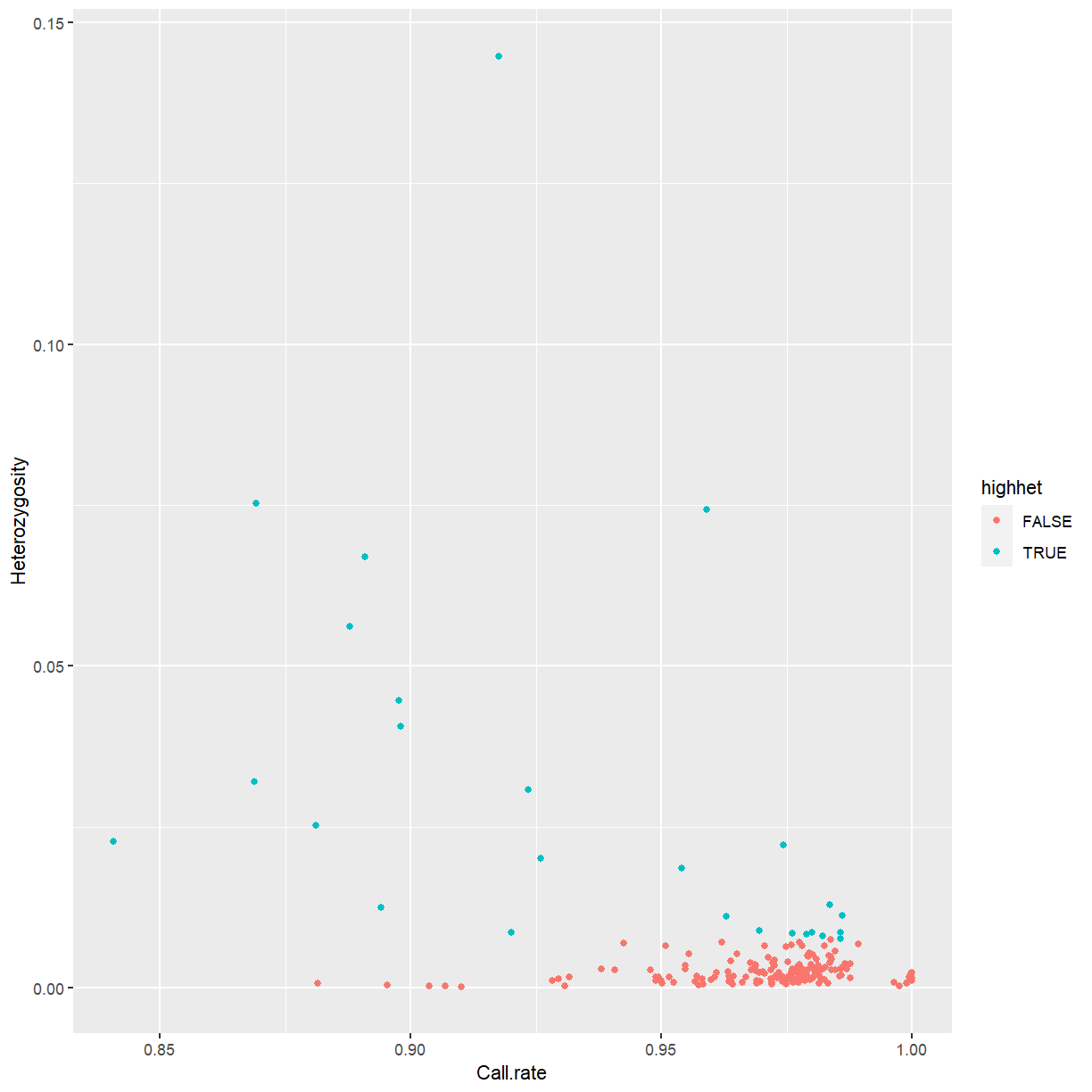
mat2 <- mat[!highhet,]
mat2
A SnpMatrix with 172 rows and 21136 columns
Row names: 2005-4 ... german_EZ5
Col names: 1-21094080 ... 1-23395848
Now we’ll look at stats for the markers.
marker_stats <- col.summary(mat2)
ggplot(marker_stats, aes(x = MAF)) +
geom_histogram()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
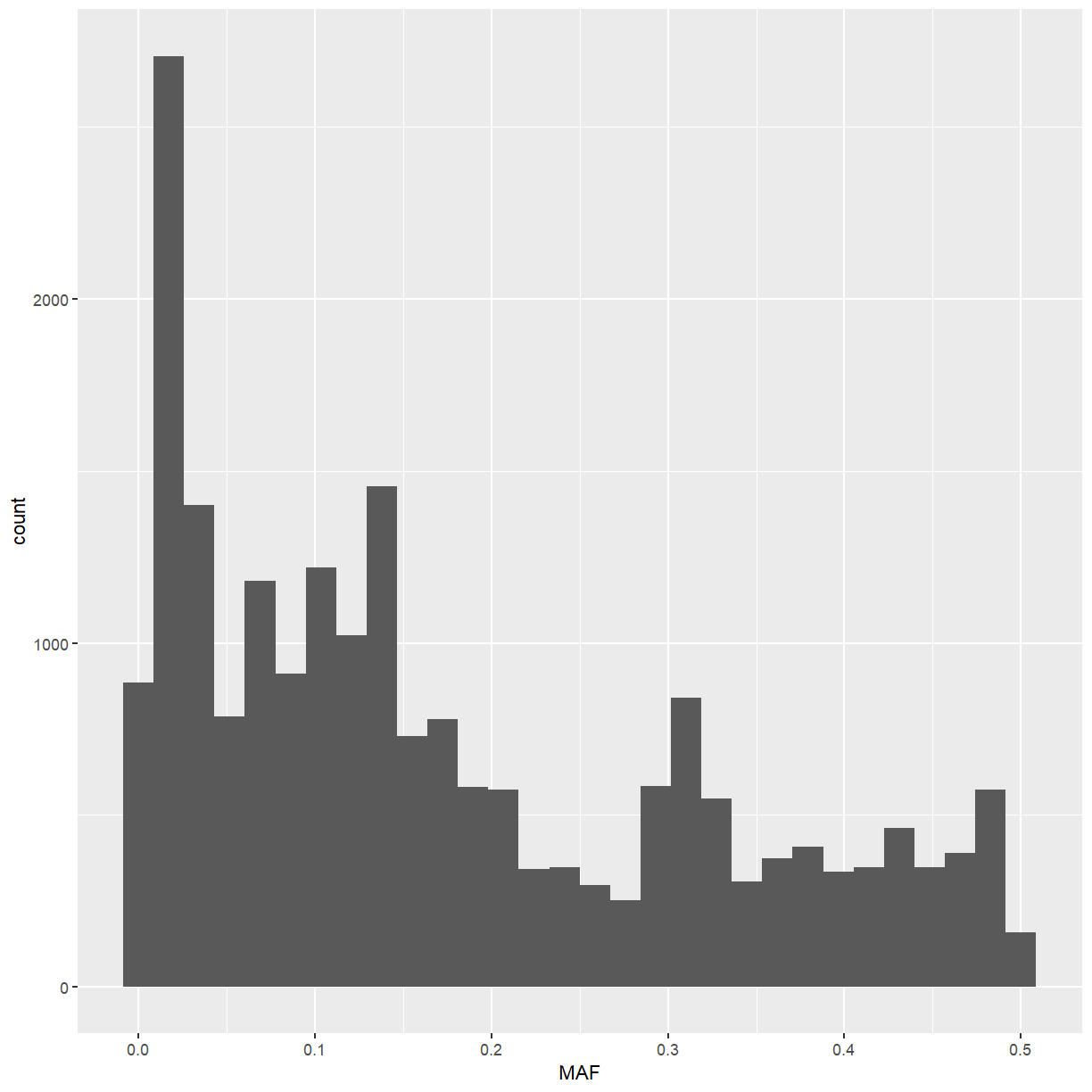
The minor allele frequency has a somewhat strange distribution, but that may have to do with the structure of the various breeding populations used in this dataset.
Let’s look at ratio of observed to expected heterozygosity.
marker_stats <- dplyr::mutate(marker_stats, Ho.He = P.AB / (2 * MAF * (1 - MAF)))
ggplot(marker_stats, aes(x = Ho.He)) +
geom_histogram()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 98 rows containing non-finite values (stat_bin).
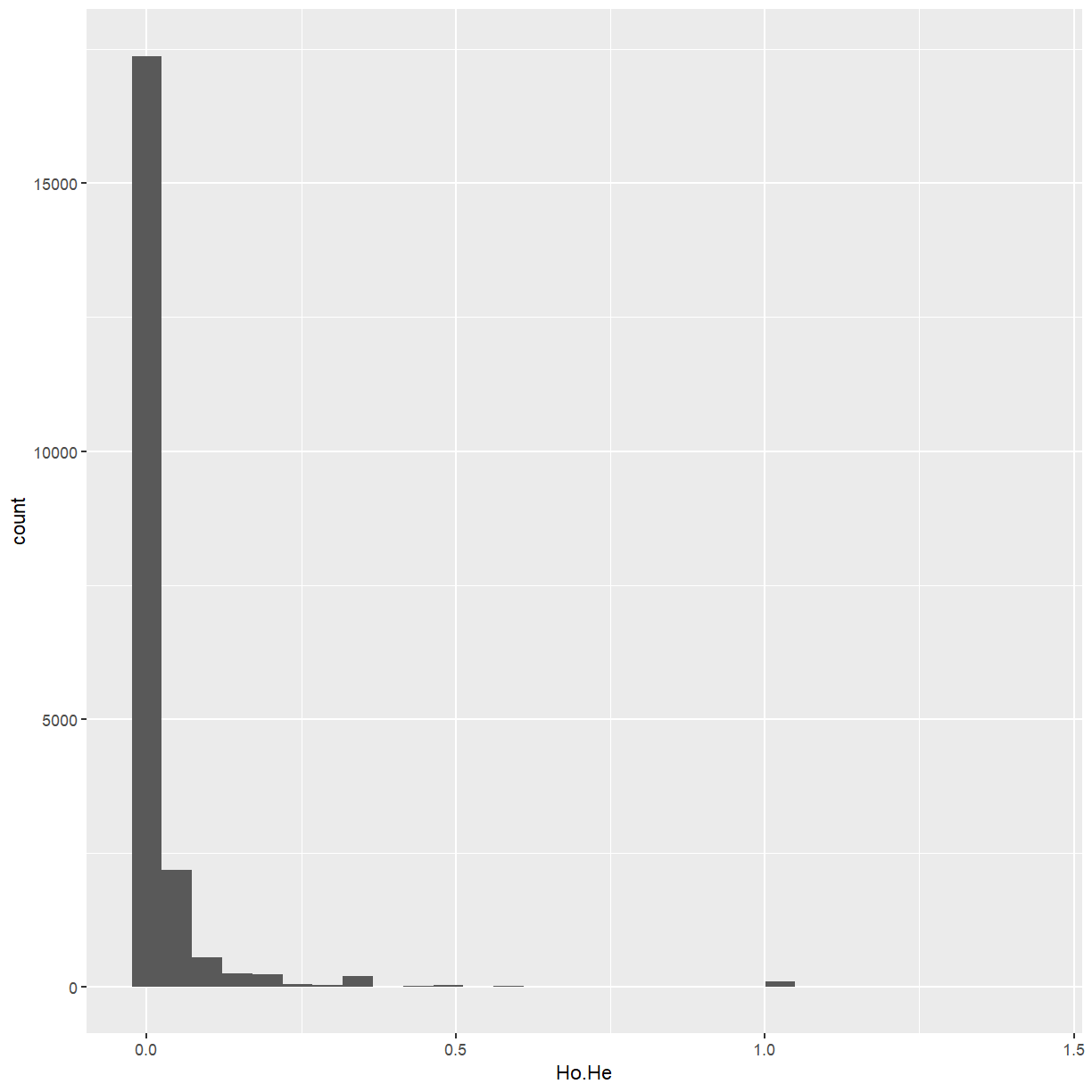
We have a few markers that are much more heterozygous than the rest. Some come out as
NA because the minor allele frequency is zero, and we may as well discard those too.
highhet2 <- isOutlier(marker_stats$Ho.He, type = "higher")
Warning in .get_med_and_mad(metric, batch = batch, subset = subset,
share.medians = share.medians, : missing values ignored during outlier detection
highhet2[is.na(highhet2)] <- TRUE
mat3 <- mat2[, !highhet2]
mat3
A SnpMatrix with 172 rows and 15104 columns
Row names: 2005-4 ... german_EZ5
Col names: 1-21094080 ... 1-23395224
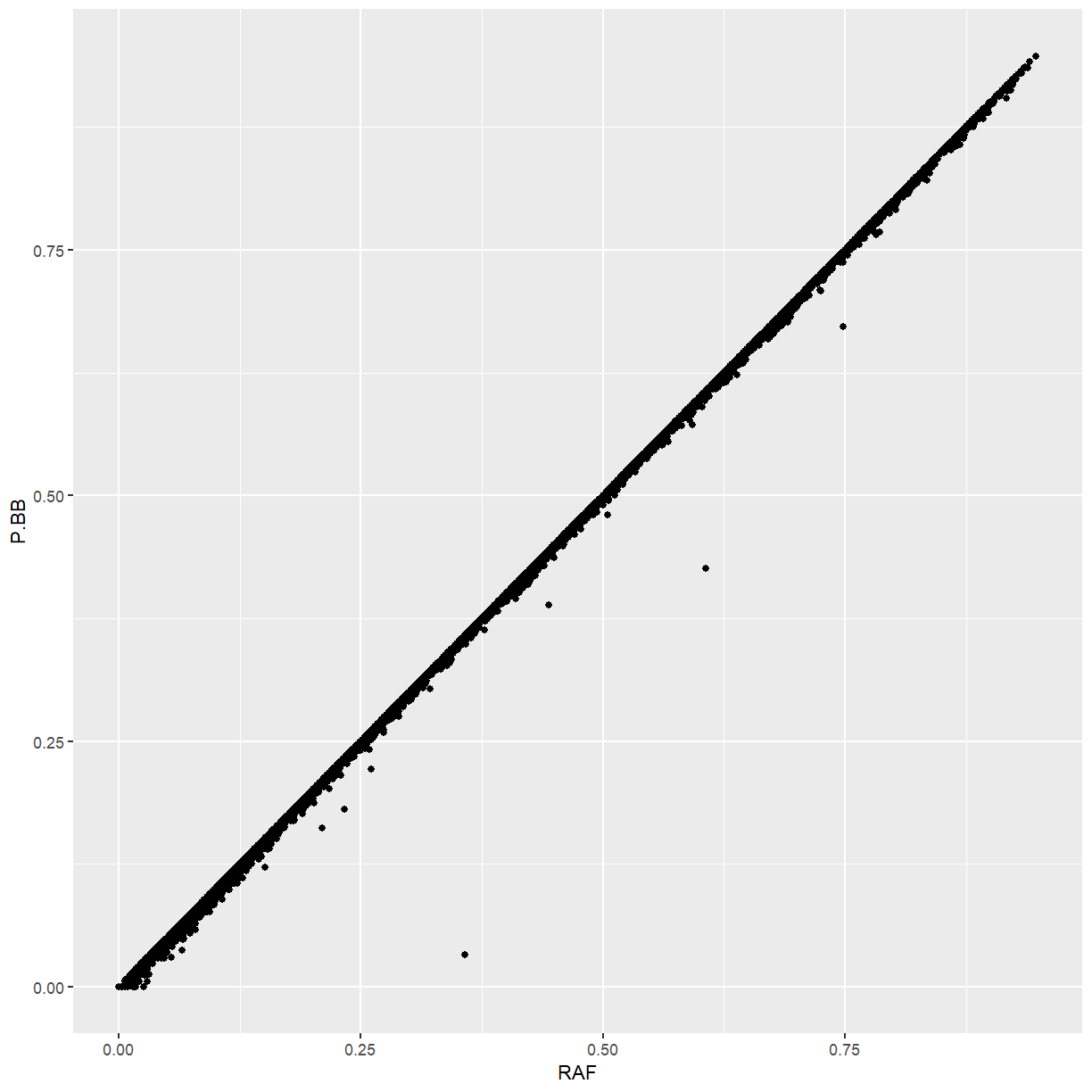
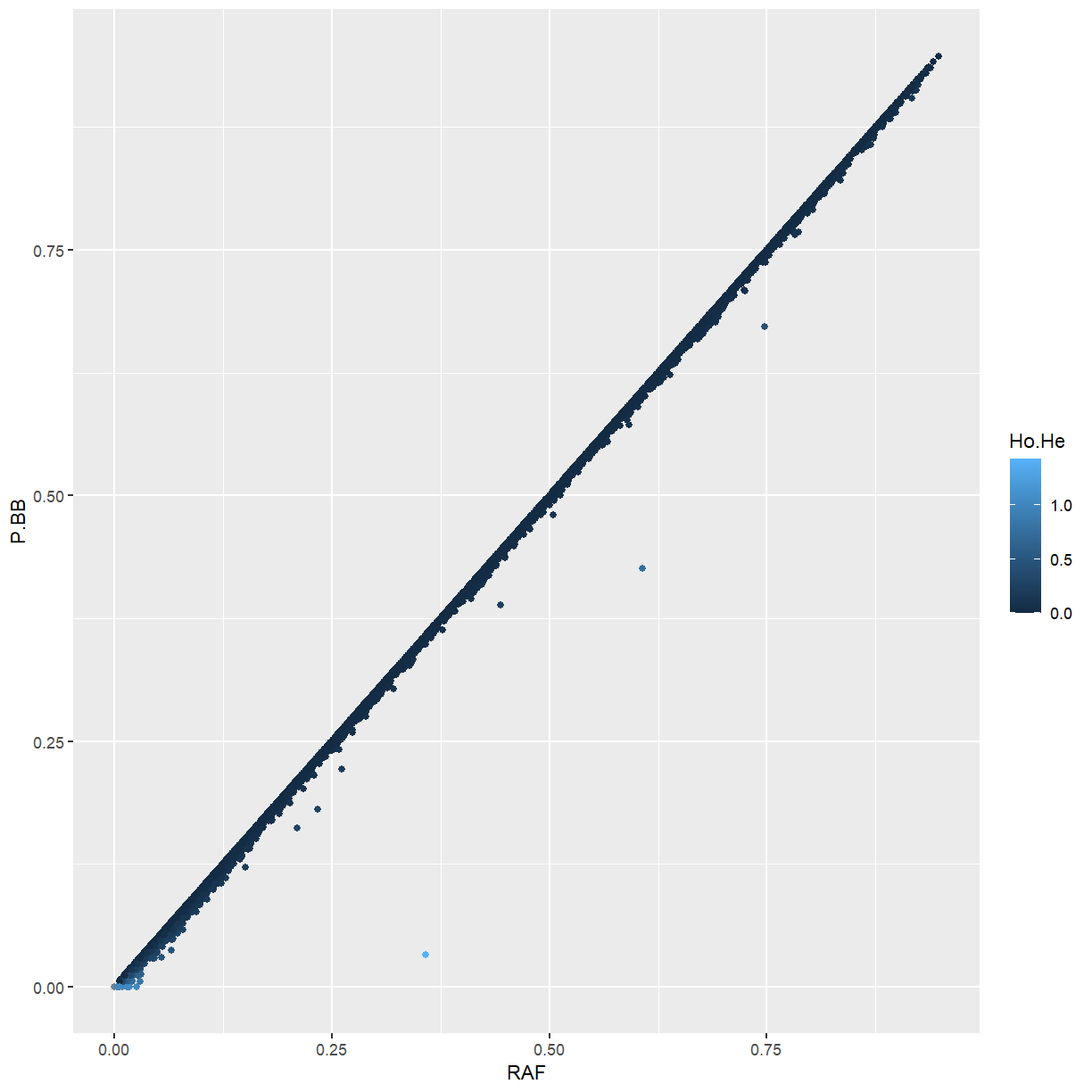
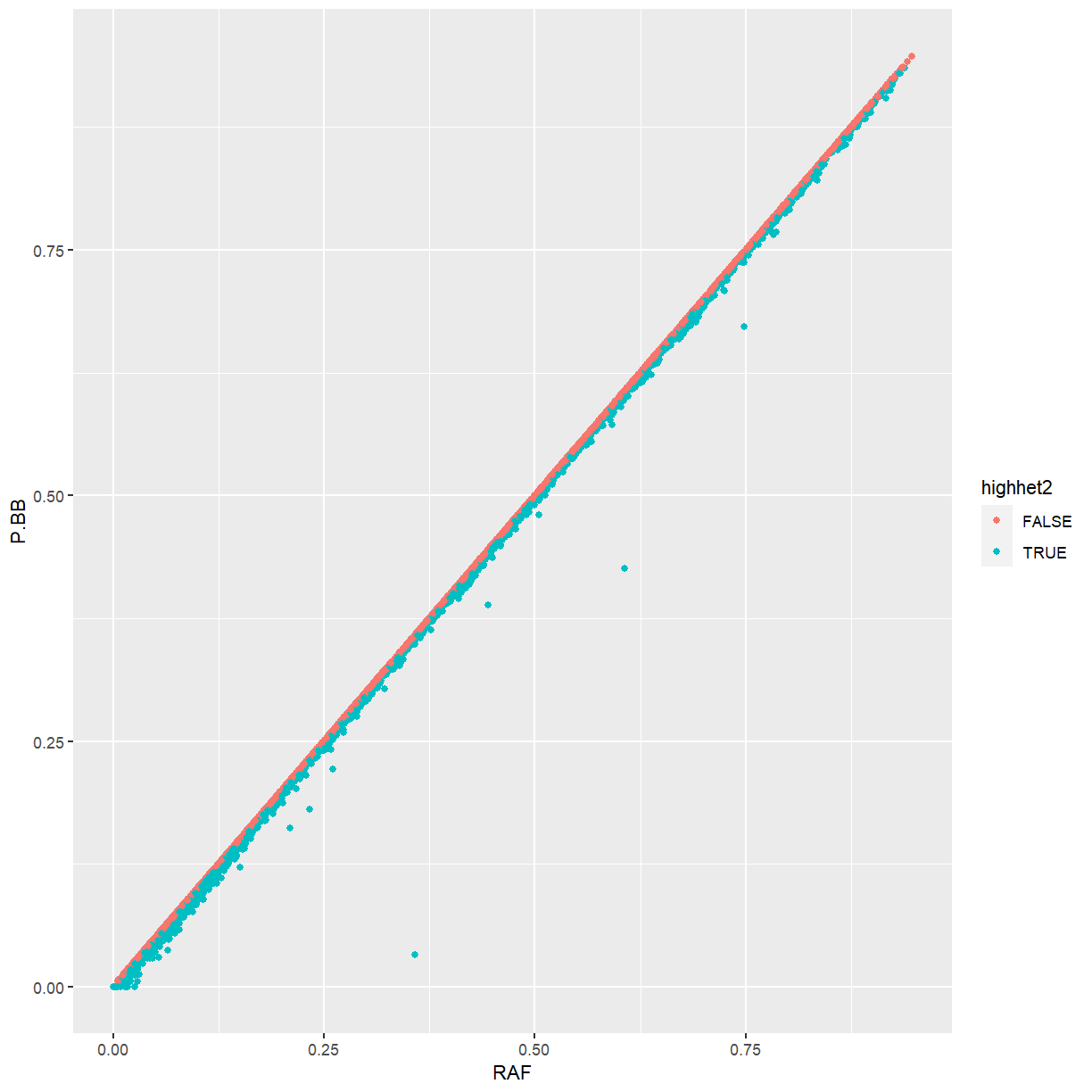
Challenge: P.BB vs. RAF
Using our
marker_statsdata frame andggplot, make a graph ofP.BBvs.RAF. What is your interpretation of this plot? For an extra challenge, color the points byHo.Heor byhighhet2.Solution
ggplot(marker_stats, aes(x = RAF, y = P.BB)) + geom_point()
ggplot(marker_stats, aes(x = RAF, y = P.BB, color = Ho.He)) + geom_point()
ggplot(marker_stats, aes(x = RAF, y = P.BB, color = highhet2)) + geom_point()
Because maize is highly inbred, the frequency of the ALT allele is almost identical the the frequency of homozygotes for the ALT allele. Markers that differ from that pattern tend to be ones that we identified as being too heterozygous.
Linkage Disequilibrium
If we know how much linkage disequilibrium is in our dataset, we know how far
away from a significant SNP to search for candidate genes. Although not shown
here, it can also be helpful if you want to prune redundant markers. We’ll
calculate it with the ld function and visualize the first 500 markers.
mydepth <- 100 # how many adjacent markers to look at
myLD <- ld(mat3, depth = mydepth, stats = "R.squared", symmetric = FALSE)
image(myLD[1:500, 1:500], lwd = 0)

There are some loose blocks of LD, but also a lot of adjacent markers that are not in LD with each other.
We’ll get the physical distance between markers based on an approach demonstrated
in vignette("ld-vignette", package = "snpStats").
pos <- start(rowRanges(mydata)[colnames(mat3)])
nSNP <- length(pos)
diags <- vector("list", mydepth)
for (i in 1:mydepth) diags[[i]] <- pos[(i+1):nSNP] - pos[1:(nSNP-i)]
physical_distance <- bandSparse(nSNP, k=1:mydepth, diagonals=diags)
Now we’ll plot LD vs. physical distance.
physical_distance_vals <- physical_distance@x
LD_vals <- myLD@x
random_subset <- sample(which(physical_distance_vals < 2e5), 5000)
ggplot(mapping = aes(x = physical_distance_vals[random_subset],
y = LD_vals[random_subset])) +
labs(x = "Distance in bp", y = "R-squared") +
geom_point(alpha = 0.1) +
geom_smooth(formula = y ~ log(x)) +
geom_vline(xintercept = c(2000, 5000), color = "red", lty = 2)
`geom_smooth()` using method = 'gam'
Warning: Removed 25 rows containing non-finite values (stat_smooth).
Warning: Removed 25 rows containing missing values (geom_point).
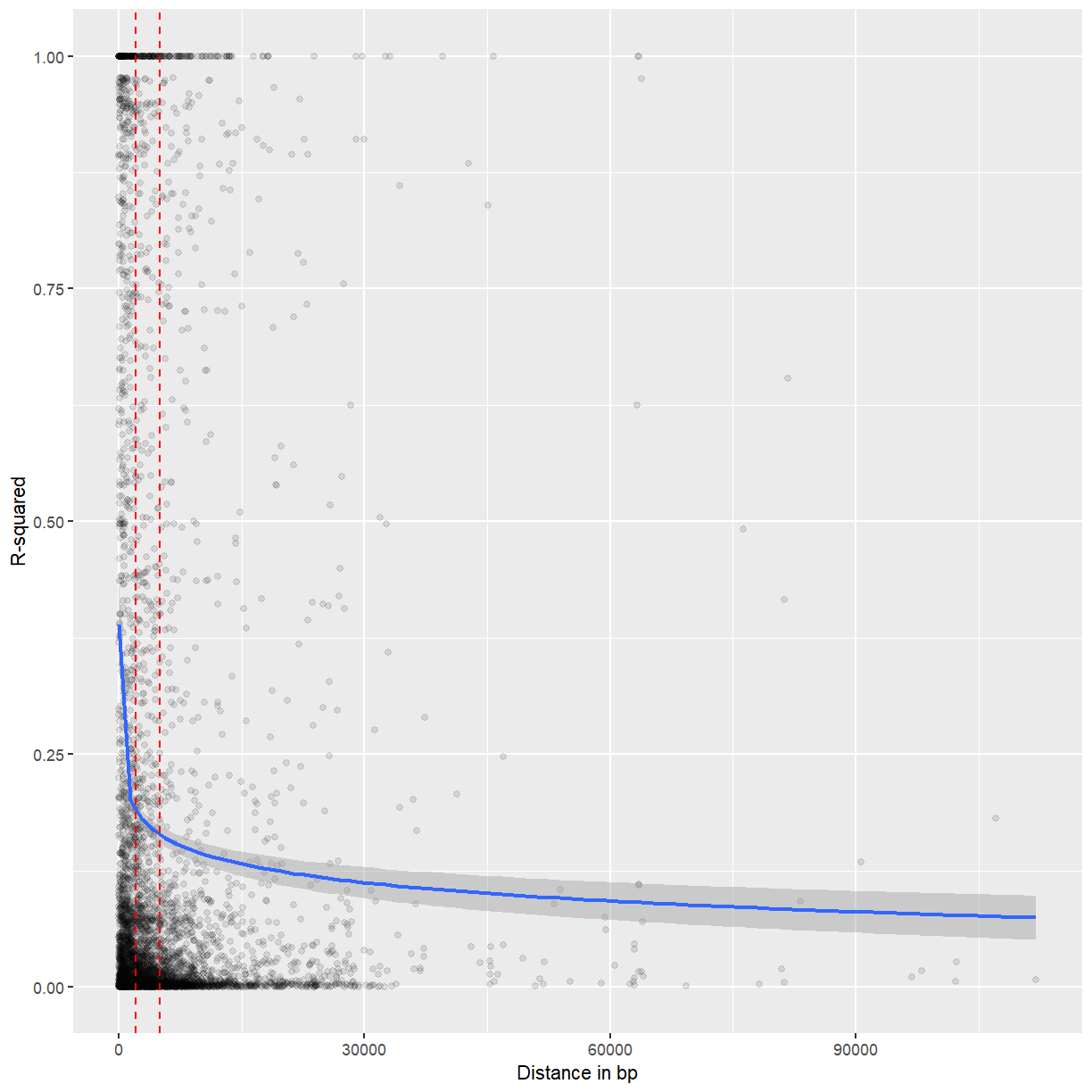
Most but not all LD seems to decay after 2-5 kb.
Principal components analysis
We should visualize the population structure of the dataset. This can help identify groupings that should be accounted for in GWAS or other analysis. It can also help to identify groups of samples that are very different from the rest due to species misidentification or technical issues.
First, we’ll use the xxt function to fill in missing data and multiply the
genotype matrix by itself transposed.
my_xxt <- xxt(mat3)
Then, we’ll use eigen to perform PCA.
my_pca <- eigen(my_xxt, symmetric = TRUE)
We’ll visualize the percentage variation explained by each axis.
percent_variation <- round(my_pca$values/sum(my_pca$values) * 100, 2)
plot(percent_variation)
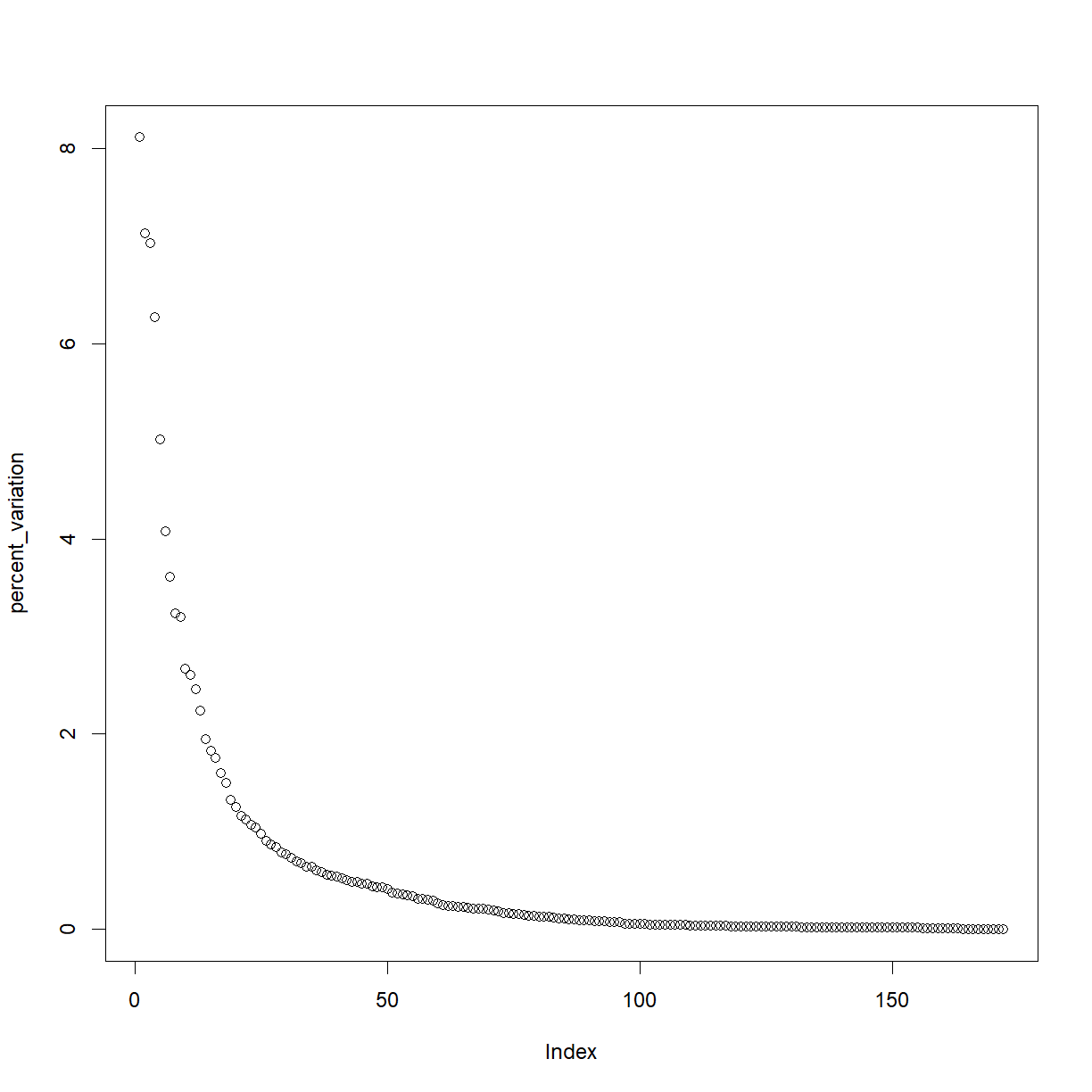
The cutoff is arbitrary, but probably at least the first six PCs are worth investigating. We’ll make a function to plot PCs by number.
plotPCs <- function(x, y, eigenvect = my_pca$vectors,
pct_var = percent_variation){
ggplot(mapping = aes(x = eigenvect[,x], y = eigenvect[,y])) +
geom_point() +
labs(x = paste0("PC", x, " (", pct_var[x], "%)"),
y = paste0("PC", y, " (", pct_var[y], "%)"))
}
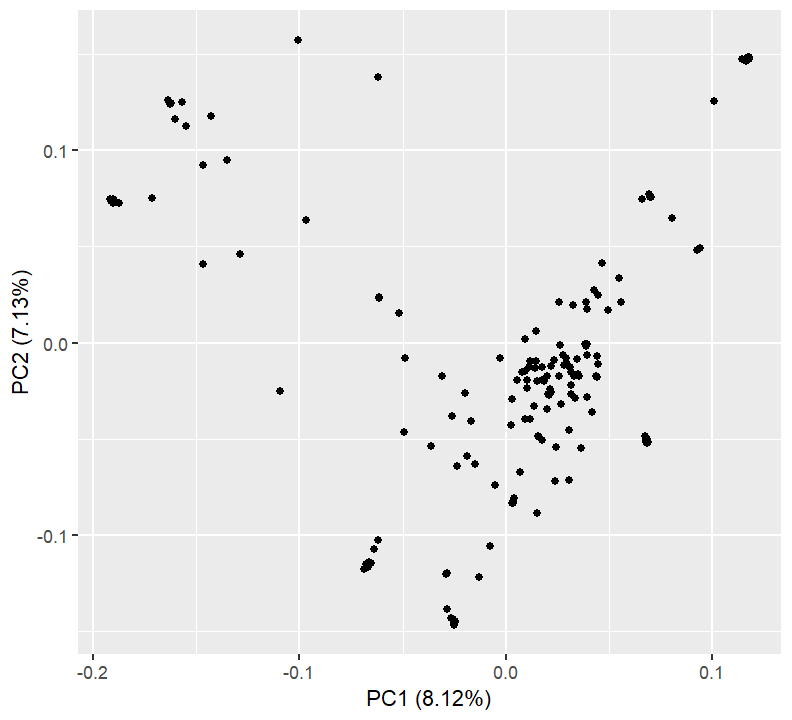
plotPCs(1, 2)
plotPCs(3, 4)

plotPCs(5, 6)
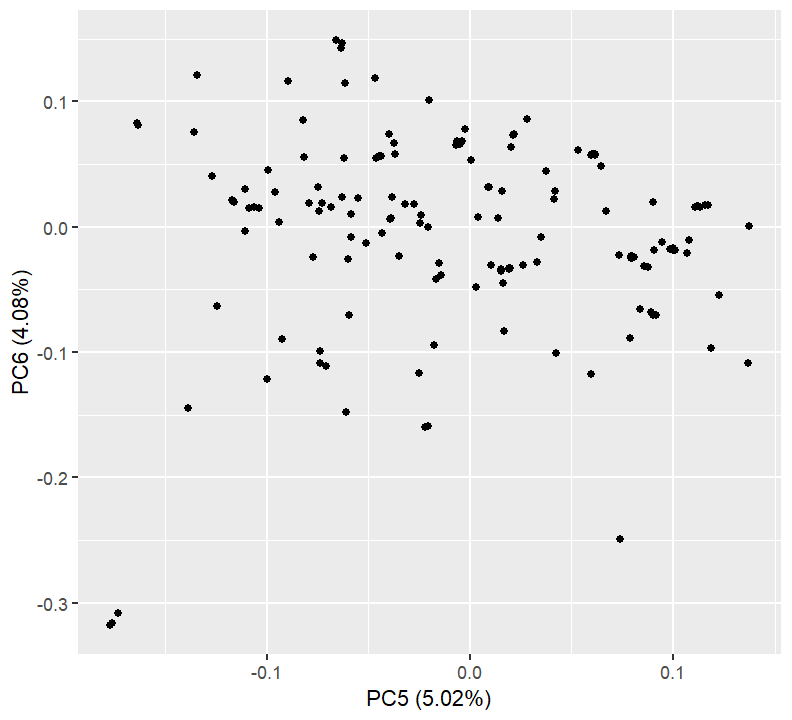
Nothing here is too concerning. We might want to export the PCA values and see what individuals get separated out on which axes.
pca_tab <- data.frame(Sample = rownames(mat3),
my_pca$vectors[,1:6])
colnames(pca_tab)[-1] <- paste0("PC", 1:6)
pca_tab %>% dplyr::filter(PC1 < -0.05) %>%
dplyr::select(Sample, PC1, PC2)
Sample PC1 PC2
1 2005-4 -0.13525727 0.09480374
2 207 -0.19065895 0.07388037
3 78004 -0.06547668 -0.11441417
4 83IBI3 -0.18867283 0.07281932
5 9058 -0.16032711 0.11623400
6 CT109 -0.15518523 0.11236514
7 D20 -0.16232946 0.12437606
8 D857 -0.16351580 0.12604026
9 E588 -0.15697666 0.12490506
10 FR14 -0.06776477 -0.11502232
11 H114 -0.12896322 0.04600527
12 HD568 -0.19024578 0.07434204
13 huangchanga -0.14306171 0.11791188
14 LH1 -0.19111678 0.07353775
15 LP1 -0.06212702 -0.10273509
16 N192 -0.06209931 0.13797158
17 N42 -0.10046524 0.15733457
18 NS501 -0.06623449 -0.11428079
19 Pa91 -0.06373167 -0.10726813
20 PHG50 -0.18753704 0.07263444
21 PHG83 -0.19041778 0.07249585
22 PHJ31 -0.10922145 -0.02493382
23 PHM10 -0.19191092 0.07482949
24 PHN11 -0.18990018 0.07401101
25 R1656 -0.16294629 0.12403325
26 ZEAxppRBMDIAAPEI-6 -0.06883696 -0.11787323
27 282set_A634 -0.06693384 -0.11678946
28 282set_A654 -0.05176967 0.01533634
29 282set_B103 -0.14677217 0.04077557
30 282set_CI64 -0.17143190 0.07489318
31 282set_OH7B -0.14651879 0.09233454
32 282set_Pa875 -0.06159597 0.02382521
33 282set_Wf9 -0.06138572 0.02309199
34 german_FF0721H-7 -0.09706747 0.06381097
write.csv(pca_tab, file = "maize_pca.csv", row.names = FALSE)
Challenge: Find those accessions
PCs 3 and 4 separate out a tight cluster of individuals, in the upper left of the plot. What are the identities of these?
Solution
pca_tab %>% dplyr::filter(PC3 < -0.17) %>% dplyr::select(Sample, PC1, PC2, PC3, PC4)Sample PC1 PC2 PC3 PC4 1 CAUMo17 0.06846645 -0.05034345 -0.2097394 0.1410231 2 LH128 0.06781703 -0.05170517 -0.2029908 0.1412591 3 LH51 0.06746680 -0.04877299 -0.2071386 0.1387211 4 LH60 0.06793352 -0.05081062 -0.2060974 0.1407863 5 SG17 0.06832035 -0.05228311 -0.2027568 0.1415698 6 ZEAxppRCODIAAPEI-9 0.06872508 -0.05148261 -0.2081216 0.1423601 7 282set_CI187-2 0.06828446 -0.05171065 -0.2046271 0.1430273
Key Points
The snpStats package can convert genotypes to numeric format and calculate statistics.